Zwei Zahlen a und b heißen kommensurabel, d.h. mit gleichem Maß meßbar, wenn sie ganzzahlige Vielfache einer dritten Zahl c sind. Aus 
folgt dann
 |
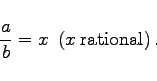(1.10) |
Im entgegengesetzten Falle sind a und b inkommensurabel.
| Beispiel A |
|
Die Länge einer Diagonale und die Seitenlänge eines Quadrates sind inkommensurabel, weil sie die irrationale Zahl |
| Beispiel B |
|
Strecken, die gemäß dem Goldenen Schnitt bemessen werden, sind inkommensurabel, weil dieser die irrationale Zahl |
