Inhalt Index DeskTop Bronstein
![]()
![]() Arithmetik Algebraische und transzendente Gleichungen Gleichungen 1. bis 4. Grades Gleichungen 3. Grades (kubische Gleichungen)
Arithmetik Algebraische und transzendente Gleichungen Gleichungen 1. bis 4. Grades Gleichungen 3. Grades (kubische Gleichungen)
Durch die Substitution y=u+v geht (1.155b) in
| u3+v3+(u+v)(3uv+3p)+2q=0 | (1.159a) |
über. Diese Gleichung ist sicher dann erfüllt,wenn
 |
(1.159b) |
gilt. Schreibt man diese Gleichungen in der Form
 |
(1.159c) |
dann sind von den beiden unbekannten Größen u3 und v3 Summe und Produkt bekannt, so daß sie auf Grund des VIETAschen Wurzelsatzes bzw. wegen (1.151) als Lösungen der quadratischen Gleichung
| w2-(u3+v3)w+u3v3=w2+2qw-p3 = 0 | (1.159d) |
 |
(1.159e) |
so daß sich für die Lösungen y der Gleichung (1.155b) die CARDANOsche Formel
 |
(1.159f) |
ergibt. Wegen der Dreideutigkeit jeder 3. Wurzel wären neun verschiedene Fälle möglich, die sich wegen uv=-p auf die folgenden drei Lösungen reduzieren:
 |
(1.159g) |
 |
(1.159h) |
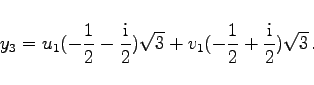 |
(1.159i) |
| Beispiel |
|
y3 +6y+2 = 0 mit |