Variationsaufgaben in Parameterdarstellung

Bei manchen Variationsaufgaben ist es zweckmäßig, die Extremale nicht in der expliziten Form y=y(x) anzugeben, sondern von deren Parameterdarstellung

(10.38)

auszugehen, wobei t1 und t2 die den Punkten (a,A) und (b,B) entsprechenden Parameterwerte sein sollen. Die einfache Variationsaufgabe lautet dann

(10.39a)

mit den Randbedingungen

(10.39b)

Mit und werden, wie bei der Parameterdarstellung üblich, die Ableitungen von x und y nach dem Parameter t bezeichnet.
Das Variationsproblem (10.39a) ist nur dann sinnvoll, wenn der Wert des Integrals von der Parameterdarstellung der Extremale unabhängig ist. Es gilt: Damit das Integral in (10.39a) von der Parameterdarstellung der Kurve, die die Punkte (a,A) und (b,B) verbindet, unabhängig ist, muß F eine positiv homogene Funktion sein, d.h., es muß

(10.40)

gelten.
Da die Variationsaufgabe (10.39a) als Spezialfall von (10.34) aufgefaßt werden kann, lauten die zugehörigen EULERschen Differentialgleichungen

(10.41)

Diese sind nicht unabhängig voneinander, sondern äquivalent der sogenannten WEIERSTRASSschen Form der EULERschen Differentialgleichung:

(10.42a)

mit

(10.42b)

Ausgehend von der Berechnung des Krümmungskreisradius R einer in Parameterdarstellung gegebenen Kurve, erfolgt die Berechnung des Krümmungskreisradius der Extremalen unter Berücksichtigung von (10.42a) gemäß

(10.42c)
Beispiel

Das isoperimetrische Problem (10.8a bis 10.8c) lautet in Parameterdarstellung
(10.43a)

mit

(10.43b)

Diese Variationsaufgabe mit Nebenbedingung geht gemäß (10.26) mit

(10.43c)

in eine Variationsaufgabe ohne Nebenbedingung über. Man sieht, das H die Bedingung (10.40) erfüllt, also eine positiv homogene Funktion vom Grade 1 ist. Weiterhin gilt

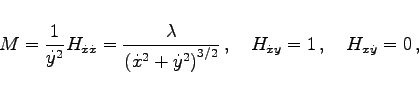(10.43d)

so daß man aus (10.42c) für den Krümmungskreisradius erhält. Da konstant ist, sind die Extremalen Kreise.