Eigenschaften linearer kompakter Operatoren

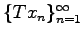Eine sequentielle Charakteristik der Kompaktheit eines Operators aus ist die folgende: Für jede beschränkte Folge aus enthält die Folge eine konvergente Teilfolge. Eine Linearkombination kompakter Operatoren ist wieder kompakt. Ist einer der Operatoren kompakt, dann sind es auch die Operatoren TU und . Falls ein BANACH-Raum ist, hat man die folgenden wichtigen Aussagen.

1. Konvergenz:

Konvergiert eine Folge von kompakten Operatoren im Raum , dann ist der Grenzwert ebenfalls ein kompakter Operator.

2. Satz von Schauder:

Ist T ein linearer stetiger Operator, dann sind T und T^* gleichzeitig kompakt (oder nicht).

3. Spektraleigenschaften eines kompakten Operators

T in einem (unendlichdimensionalen) BANACH-Raum 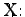Die Null gehört zum Spektrum. Jeder von Null verschiedene Punkt des Spektrums ist ein Eigenwert mit endlichdimensionalem Eigenraum , und für liegen außerhalb des Kreises stets nur endlich viele Eigenwerte von , wobei einzig die Null Häufungspunkt der Menge der Eigenwerte sein kann. Ist 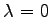kein Eigenwert von , dann ist T^-1 im Falle seiner Existenz unbeschränkt.