Inhalt Index DeskTop Bronstein
![]()
![]() Funktionalanalysis Nichtlineare Operatoren Monotone Operatoren in Banach-Räumen
Funktionalanalysis Nichtlineare Operatoren Monotone Operatoren in Banach-Räumen
Ein beliebiger Operator ![]() heißt demistetig im Punkt
heißt demistetig im Punkt ![]() , wenn für jede (in der Norm von
, wenn für jede (in der Norm von ![]() ) zu x0 konvergente Folge
) zu x0 konvergente Folge ![]() die Folge
die Folge ![]() in
in ![]() schwach zu T(x0) konvergiert. T heißt demistetig auf der Menge
schwach zu T(x0) konvergiert. T heißt demistetig auf der Menge ![]() , wenn T in jedem Punkt von D demistetig ist.
, wenn T in jedem Punkt von D demistetig ist.
In diesem Abschnitt wird eine andere Verallgemeinerung des aus der reellen Analysis bekannten Monotoniebegriffs eingeführt. Seien jetzt ![]() ein reeller BANACH-Raum,
ein reeller BANACH-Raum, ![]() sein Dual,
sein Dual, ![]() und
und ![]() ein nichtlinearer Operator. Dann heißt T monoton, wenn für
ein nichtlinearer Operator. Dann heißt T monoton, wenn für ![]() die Ungleichung
die Ungleichung ![]() gilt. Ist
gilt. Ist ![]() ein HILBERT-Raum, dann ist das Skalarprodukt gemeint, während im Falle eines BANACH-Raumes bzgl. der Bezeichnung auf Abschnitt Fortsetzung von linearen Funktionalen verwiesen wird. Der Operator T heißt streng monoton wenn es eine Konstante c > 0 gibt, so daß
ein HILBERT-Raum, dann ist das Skalarprodukt gemeint, während im Falle eines BANACH-Raumes bzgl. der Bezeichnung auf Abschnitt Fortsetzung von linearen Funktionalen verwiesen wird. Der Operator T heißt streng monoton wenn es eine Konstante c > 0 gibt, so daß ![]() für
für ![]() gilt.
gilt.
Ein Operator ![]() heißt koerzitiv, wenn
heißt koerzitiv, wenn 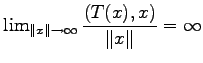 gilt.
gilt.