Inhalt Index DeskTop Bronstein
![]()
![]() Funktionalanalysis Metrische Räume Vollständige metrische Räume Einige Anwendungen des Kontraktionsprinzips
Funktionalanalysis Metrische Räume Vollständige metrische Räume Einige Anwendungen des Kontraktionsprinzips
Es werde die Differentialgleichung
mit einer stetigen Abbildung ![]() betrachtet, wobei I ein offenes Intervall aus
betrachtet, wobei I ein offenes Intervall aus ![]() und G eine offene Teilmenge aus
und G eine offene Teilmenge aus ![]() sind. Die Abbildung f genüge bezüglich x einer LIPSCHITZ-Bedingung, d.h., es gibt eine positive Konstante L mit
sind. Die Abbildung f genüge bezüglich x einer LIPSCHITZ-Bedingung, d.h., es gibt eine positive Konstante L mit
 |
(12.71) |
wobei ![]() die euklidische Metrik in
die euklidische Metrik in ![]() bezeichnet (unter Verwendung der Norm, gilt die Beziehung (12.81)
bezeichnet (unter Verwendung der Norm, gilt die Beziehung (12.81) ![]() . Sei
. Sei ![]() ein beliebiger Punkt. Dann gibt es solche Zahlen
ein beliebiger Punkt. Dann gibt es solche Zahlen ![]() und r>0 so, daß die Menge
und r>0 so, daß die Menge ![]() in I x G liegt. Seien
in I x G liegt. Seien ![]() und
und  . Dann existiert eine Zahl
. Dann existiert eine Zahl ![]() , so daß für jedes
, so daß für jedes ![]() mit
mit ![]() das Anfangswertproblem
das Anfangswertproblem
genau eine (lokale) Lösung ![]() besitzt, d.h.
besitzt, d.h. ![]() für
für ![]() und
und ![]() . Die Lösung dieses Anfangswertproblems ist äquivalent zur Lösung der Integralgleichung
. Die Lösung dieses Anfangswertproblems ist äquivalent zur Lösung der Integralgleichung
Bezeichnet jetzt ![]() die abgeschlossene Kugel
die abgeschlossene Kugel ![]() des in der Metrik
des in der Metrik
 |
(12.74) |
vollständigen metrischen Raumes ![]() , dann ist
, dann ist ![]() mit der induzierten Metrik selbst ein vollständiger metrischer Raum. Ist
mit der induzierten Metrik selbst ein vollständiger metrischer Raum. Ist ![]() der durch
der durch
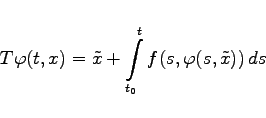 |
(12.75) |
definierte Operator, dann ergibt sich die Lösung der Integralgleichung (12.73) als eindeutiger Fixpunkt des Operators ![]() , der sogar iterativ erzeugt werden kann.
, der sogar iterativ erzeugt werden kann.