Inhalt Index DeskTop Bronstein
![]()
![]() Funktionalanalysis Stetige lineare Operatoren und Funktionale Elemente der Spektraltheorie linearer Operatoren
Funktionalanalysis Stetige lineare Operatoren und Funktionale Elemente der Spektraltheorie linearer Operatoren
Bei Untersuchungen zur Lösbarkeit von Gleichungen ist man bestrebt, das Problem auf die Form
Sei T ein linearer, im allgemeinen unbeschränkter Operator im BANACH-Raum ![]() . Die Menge
. Die Menge ![]() aller komplexen Zahlen, für die
aller komplexen Zahlen, für die ![]() gilt, heißt Resolventenmenge und der Operator
gilt, heißt Resolventenmenge und der Operator ![]() Resolvente. Sei jetzt T ein beschränkter linearer Operator in einem komplexen BANACH-Raum
Resolvente. Sei jetzt T ein beschränkter linearer Operator in einem komplexen BANACH-Raum ![]() . Dann gelten die Aussagen:
. Dann gelten die Aussagen:
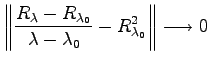 , wenn
, wenn