Inhalt Index DeskTop Bronstein
![]()
![]() Funktionalanalysis Stetige lineare Operatoren und Funktionale Beschränktheit, Norm und Stetigkeit linearer Operatoren
Funktionalanalysis Stetige lineare Operatoren und Funktionale Beschränktheit, Norm und Stetigkeit linearer Operatoren
Für zwei lineare (stetige) Operatoren ![]() sind die Summe S+T und das Vielfache
sind die Summe S+T und das Vielfache ![]() punktweise erklärt:
punktweise erklärt:
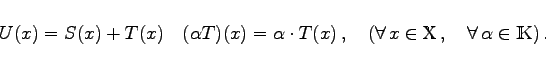 |
(12.136) |
Die Menge ![]() , häufig auch mit
, häufig auch mit ![]() bezeichnet, aller linearen stetigen Operatoren T aus
bezeichnet, aller linearen stetigen Operatoren T aus ![]() in
in ![]() wird so ein Vektorraum, auf dem sich
wird so ein Vektorraum, auf dem sich ![]() (12.131) als Norm erweist. Dadurch wird
(12.131) als Norm erweist. Dadurch wird ![]() ein normierter Raum und, falls
ein normierter Raum und, falls ![]() ein BANACH-Raum ist, sogar ein BANACH-Raum. Insbesondere sind also die Axiome
ein BANACH-Raum ist, sogar ein BANACH-Raum. Insbesondere sind also die Axiome ![]() bis
bis ![]() und
und ![]() bis
bis ![]() erfüllt.
erfüllt.
Ist ![]() , dann kann man für zwei beliebige Elemente
, dann kann man für zwei beliebige Elemente ![]() durch
durch
das Produkt definieren, das den Axiomen ![]() bis
bis ![]() aus normierte Algebren sowie der Verträglichkeitsbedingung (12.100) mit der Norm genügt und so
aus normierte Algebren sowie der Verträglichkeitsbedingung (12.100) mit der Norm genügt und so ![]() zu einer (im allgemeinen nichtkommutativen) normierten und, falls
zu einer (im allgemeinen nichtkommutativen) normierten und, falls ![]() BANACH-Raum ist, zu einer BANACH-Algebra macht. Damit sind für jeden Operator
BANACH-Raum ist, zu einer BANACH-Algebra macht. Damit sind für jeden Operator ![]() die Potenzen
die Potenzen
definiert, wobei I der identische Operator ![]() ist. Es gilt
ist. Es gilt
und außerdem existiert stets der (endliche) Grenzwert
der Spektralradius des Operators T heißt und den Beziehungen
genügt, wobei T* der zu T adjungierte Operator ist (s. auch (12.175)).
Im Falle der Vollständigkeit von ![]() hat der Operator
hat der Operator ![]() für
für ![]() die Darstellung in Form der NEUMANNschen Reihe
die Darstellung in Form der NEUMANNschen Reihe
die für ![]() in der Operatornorm von
in der Operatornorm von ![]() konvergiert.
konvergiert.
(S. auch Konvergenz der NEUMANNschen Reihe).