Man kann die JACOBIschen Funktionen in die komplexe Z-Ebene analytisch fortsetzen. Die Funktionen snz, cnz und dnz sind dann meromorphe Funktionen, d.h., sie besitzen außer Polstellen keine weiteren Singularitäten. Außerdem sind sie doppelperiodisch: Jede dieser Funktionen f(z) hat genau 2 Perioden 
und 
mit
 |
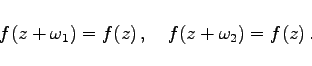(14.104) |
Dabei sind und zwei beliebige komplexe Zahlen, deren Quotient nicht reell ist. Aus (14.62) folgt die allgemeine Formel
 |
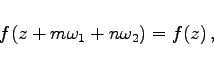(14.105) |
wobei m und n beliebige ganze Zahlen sind. Meromorphe doppelperiodische Funktionen heißen elliptische Funktionen. Die Menge
 |
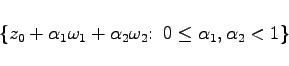(14.106) |
mit beliebigen festen 
heißt Periodenparallelogramm der elliptischen Funktion. Ist diese im Periodenparallelogramm (s. Abbildung) beschränkt, dann ist sie eine Konstante.
| Beispiel |
|
Die JACOBIschen Funktionen (14.103a) und (14.103b) sind elliptische Funktionen. Die Amplitudenfunktion (14.102b) ist keine elliptische Funktion. |