F(p) - eine absolut konvergente Reihe

Wenn F(p) in eine für | p | > R absolut konvergente Reihe der Form

entwickelt werden kann, wobei die eine beliebig aufsteigende Zahlenfolge bilden, so ist eine gliedweise Rücktransformation möglich:

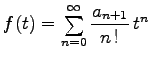Mit ist die Gammafunktion bezeichnet. Speziell erhält man für , d.h. , die Reihe , die für alle reellen und komplexen t konvergiert. Außerdem ist eine Abschätzung in der Form ) möglich.

Beispiel

.
Nach gliedweiser Transformation in den Oberbereich erhält man
     (BESSEL-Funktion 0. Ordnung).