Umkehrintegral

Die Umkehrformel

stellt ein Integral mit komplexem Weg über eine in gewissen Gebieten analytische Funktion dar, auf das solche Methoden der Integration im Komplexen wie die Residuenrechnung oder die Verformung des Integrationsweges nach dem Satz von CAUCHY anwendbar sind.

Beispiel

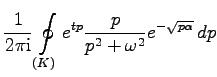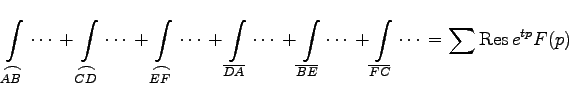ist wegen des Anteiles doppeldeutig. Deshalb wird folgender Integrationsweg gewählt (s. Abbildung):

Nach dem Lemma von JORDAN verschwinden die Integralteile über und für . Auf dem Kreisbogen (Radius ) bleibt der Integrand beschränkt, und die Länge des Integrationsweges konvergiert gegen Null für ; daher verschwindet dieser Integralbeitrag. Es bleibt das Integral über die beiden horizontalen Strecken und zu untersuchen, wobei das obere und untere Ufer der negativen reellen Achse zu berücksichtigen sind:
.
Damit erhält man endgültig:
.