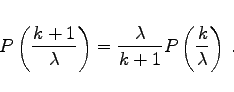Poisson-Verteilung
Die Verteilung einer diskreten Zufallsveränderlichen  , bei der
, bei der
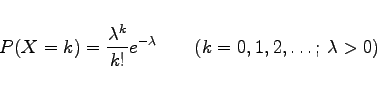 |
(16.68) |
ist, heißt POISSON-Verteilung mit den Parametern  . Es gilt:
. Es gilt:
- 1. Erwartungswert und Streuung:
-
 |
(16.69a) |
 |
(16.69b) |
- 2. Summe von POISSON-verteilten Zufallsgrößen:
- Sind X1 und X2 unabhängige, POISSON-verteilte Zufallsveränderliche mit den Parametern
 bzw.
bzw.  , so ist auch X = X1 + X2 eine POISSON-verteilte Zufallsveränderliche mit dem Parameter
, so ist auch X = X1 + X2 eine POISSON-verteilte Zufallsveränderliche mit dem Parameter  .
.
- 3. Rekursionsformel:
-
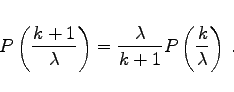 |
(16.69c) |
- 4. Zusammenhang zwischen POISSON- und Binomialverteilung:
- Die POISSON-Verteilung geht aus einer Folge von binomialverteilten Zufallsveränderlichen Xn mit den Parametern
 durch den Grenzübergang
durch den Grenzübergang  hervor, wenn man
hervor, wenn man  mit n so variiert, daß
mit n so variiert, daß  bleibt. Für
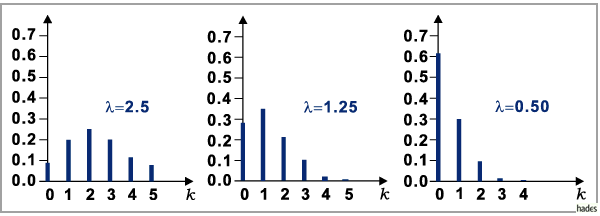
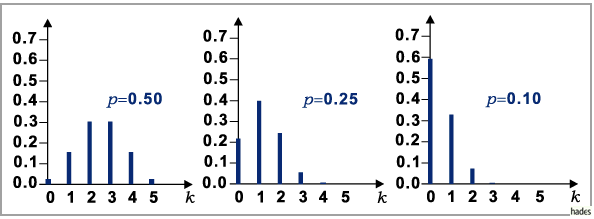
bleibt. Für  kann die Binomialverteilung mit im allgemeinen ausreichender Genauigkeit durch die POISSON-Verteilung ersetzt werden, deren Auswertung einfacher ist. Zahlenwerte für die POISSON-Verteilung enthält die Tabelle POISSON-Verteilung. In der folgenden Abbildung sind drei POISSON-Verteilungen für
kann die Binomialverteilung mit im allgemeinen ausreichender Genauigkeit durch die POISSON-Verteilung ersetzt werden, deren Auswertung einfacher ist. Zahlenwerte für die POISSON-Verteilung enthält die Tabelle POISSON-Verteilung. In der folgenden Abbildung sind drei POISSON-Verteilungen für  und 0,5 dargestellt. Die Parameter entsprechen den Parametern der anschließend zum Vergleich dargestellten drei Binomialverteilungen und drei hypergeometrischen Verteilung.
und 0,5 dargestellt. Die Parameter entsprechen den Parametern der anschließend zum Vergleich dargestellten drei Binomialverteilungen und drei hypergeometrischen Verteilung.

- 5. Anwendungen
- (s. auch POISSON-Prozesse): Durch die POISSON-Verteilung lassen sich z.B. beschreiben: Anzahl der Kunden, die in einem bestimmten Zeitintervall einen Laden betreten; Anzahl der Druckfehler in einem Buch; Rate der radioaktiven Zerfälle.
![]()
![]() Wahrscheinlichkeitsrechnung und Mathematische Statistik Wahrscheinlichkeitsrechnung Diskrete Verteilungen
Wahrscheinlichkeitsrechnung und Mathematische Statistik Wahrscheinlichkeitsrechnung Diskrete Verteilungen
![]() , bei der
, bei der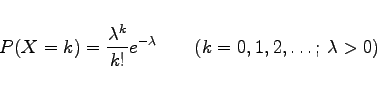
![]() . Es gilt:
. Es gilt: