Inhalt Index DeskTop Bronstein
![]()
![]() Wahrscheinlichkeitsrechnung und Mathematische Statistik Wahrscheinlichkeitsrechnung Gesetze der großen Zahlen, Grenzwertsätze
Wahrscheinlichkeitsrechnung und Mathematische Statistik Wahrscheinlichkeitsrechnung Gesetze der großen Zahlen, Grenzwertsätze
Wenn die unabhängigen Zufallsveränderlichen ![]() derselben Verteilung mit dem Erwartungswert
derselben Verteilung mit dem Erwartungswert ![]() und der Streuung
und der Streuung ![]() genügen, dann strebt die Verteilungsfunktion Fn(y) der zufälligen Veränderlichen
genügen, dann strebt die Verteilungsfunktion Fn(y) der zufälligen Veränderlichen
für ![]() gegen eine (0,1)-Normalverteilung, d.h., es ist
gegen eine (0,1)-Normalverteilung, d.h., es ist
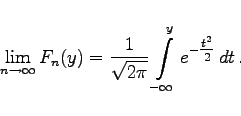 |
(16.106) |
Die Ersetzung von Fn(y) durch die (0,1)-Normalverteilung ist praktisch für n>30 möglich (s. [16.1]).
Weitere Grenzwertsätze s. [16.6], [16.10], [16.21].
| Beispiel |
|
Einer laufenden Produktion von Widerständen werden 100 Stück entnommen. Es sei bekannt, daß sämtliche Widerstandswerte unabhängig sind und derselben Verteilung mit der Streuung |