Inhalt Index DeskTop Bronstein
![]()
![]() Wahrscheinlichkeitsrechnung und Mathematische Statistik Mathematische Statistik Korrelation und Regression Lineare Regression bei zwei meßbaren Merkmalen
Wahrscheinlichkeitsrechnung und Mathematische Statistik Mathematische Statistik Korrelation und Regression Lineare Regression bei zwei meßbaren Merkmalen
Wenn zwischen den Merkmalen X und Y mit Hilfe des Korrelationskoeffizienten eine Abhängigkeit festgestellt wurde, dann besteht die nächste Aufgabe in der Ermittlung des funktionalen Zusammenhanges ![]() . Im einfachsten Falle der linearen Regression wird dabei vorausgesetzt, daß bei beliebigem, aber festem x-Wert die Zufallsgröße Y in der Grundgesamtheit normalverteilt ist mit dem Erwartungswert
. Im einfachsten Falle der linearen Regression wird dabei vorausgesetzt, daß bei beliebigem, aber festem x-Wert die Zufallsgröße Y in der Grundgesamtheit normalverteilt ist mit dem Erwartungswert
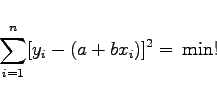 |
(16.158) |
erhält man für ![]() und
und ![]() die Schätzwerte (Näherungswerte)
die Schätzwerte (Näherungswerte)
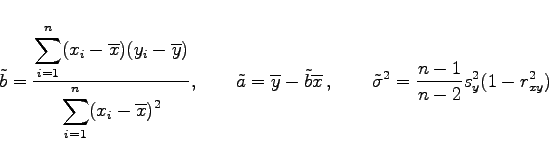 |
(16.159a) |
mit
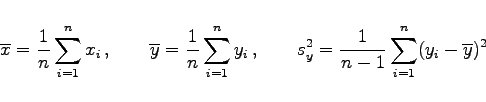 |
(16.159b) |
und dem empirischen Korrelationskoeffizienten rxy gemäß (16.156b). Die Koeffizienten ![]() und
und ![]() nennt man Regressionskoeffizienten. Die Gerade
nennt man Regressionskoeffizienten. Die Gerade ![]() heißt Regressionsgerade.
heißt Regressionsgerade.