Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Seltsame Attraktoren und Chaos
Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Seltsame Attraktoren und Chaos
Sei ![]() ein dynamisches System im metrischen Raum
ein dynamisches System im metrischen Raum ![]() mit kompakter invarianter Menge
mit kompakter invarianter Menge ![]() . Das System
. Das System ![]() bzw. die Menge
bzw. die Menge ![]() heißt chaotisch im Sinne von DEVANEY, wenn gilt:
heißt chaotisch im Sinne von DEVANEY, wenn gilt:
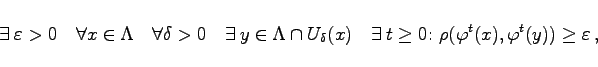 |
(17.53) |
wobei ![]() .
.
| Beispiel |
|
Bernoulli-Shift-Abbildung: Gegeben sei der Raum der einseitig unendlichen Folgen aus zwei Symbolen 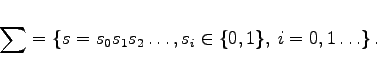  Die Shift-Abbildung ist chaotisch im Sinne von DEVANEY. |