Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Gewöhnliche Differentialgleichungen und Abbildungen Qualitative Theorie gewöhnlicher Differentialgleichungen Invariante Mannigfaltigkeiten
Dynamische Systeme und Chaos Gewöhnliche Differentialgleichungen und Abbildungen Qualitative Theorie gewöhnlicher Differentialgleichungen Invariante Mannigfaltigkeiten
Sei ![]() eine hyperbolische Ruhelage oder ein hyperbolischer periodischer Orbit von (17.1). Die stabile Mannigfaltigkeit
eine hyperbolische Ruhelage oder ein hyperbolischer periodischer Orbit von (17.1). Die stabile Mannigfaltigkeit ![]() (instabile Mannigfaltigkeit
(instabile Mannigfaltigkeit ![]() ) von
) von ![]() ist die Menge aller der Punkte des Phasenraumes, durch die Orbits verlaufen, die für
ist die Menge aller der Punkte des Phasenraumes, durch die Orbits verlaufen, die für ![]() gegen
gegen ![]() streben:
streben:
 |
(17.18) |
Stabile bzw. instabile Mannigfaltigkeiten bezeichnet man auch als Separatrixflächen.
| Beispiel |
|
In der Ebene wird die Differentialgleichung |
betrachtet. Die Lösung von (17.19a) mit Anfang (x0,y0) zur Zeit t= 0 ist durch
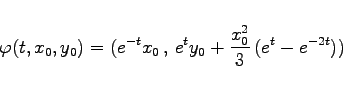 |
(17.19b) |
explizit gegeben. Für die stabile bzw. instabile Mannigfaltigkeit der Ruhelage (0,0) von (17.19a) erhält man:
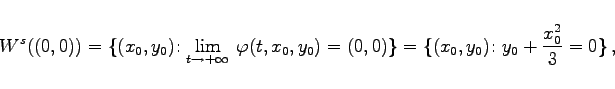
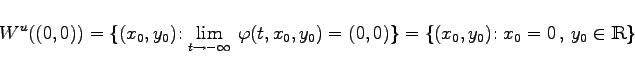
Es seien M und N zwei glatte Flächen des ![]() und LxM bzw. LxN die entsprechenden Tangentialebenen durch x an M bzw. N. Die Flächen M und N heißen transversal zueinander, wenn für alle
und LxM bzw. LxN die entsprechenden Tangentialebenen durch x an M bzw. N. Die Flächen M und N heißen transversal zueinander, wenn für alle ![]() die Beziehung
die Beziehung
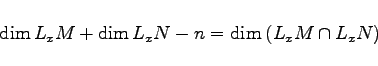
| Beispiel |
|
Für den in der folgenden Abbildung dargestellten Schnitt gilt |