Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Gewöhnliche Differentialgleichungen und Abbildungen Qualitative Theorie gewöhnlicher Differentialgleichungen Invariante Mannigfaltigkeiten
Dynamische Systeme und Chaos Gewöhnliche Differentialgleichungen und Abbildungen Qualitative Theorie gewöhnlicher Differentialgleichungen Invariante Mannigfaltigkeiten
Wichtige Eigenschaften der Separatrixflächen werden durch den Satz von HADAMARD und PERRON beschrieben:
Sei ![]() eine hyperbolische Ruhelage oder ein hyperbolischer periodischer Orbit von (17.1).
eine hyperbolische Ruhelage oder ein hyperbolischer periodischer Orbit von (17.1).
 |
(17.20a) |
bzw. den instabilen Untervektorraum
 |
(17.20b) |
| Beispiel A |
|
Nochmalige Betrachtung der Differentialgleichung (17.19a) und Benutzung für die Bestimmung einer lokalen stabilen Mannigfaltigkeit der Ruhelage (0,0) von (17.19a) den Ansatz  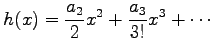 , in dem h'(0) = 0 beachtet wurde, ergibt sich durch Einsetzen und Koeffizientenvergleich , in dem h'(0) = 0 beachtet wurde, ergibt sich durch Einsetzen und Koeffizientenvergleich  und ak = 0 für und ak = 0 für |
| Beispiel B |
|
Für das System |
mit einem Parameter ![]() ist
ist ![]() ein periodischer Orbit mit den Multiplikatoren
ein periodischer Orbit mit den Multiplikatoren ![]() und
und ![]() . In Zylinderkoordinaten
. In Zylinderkoordinaten ![]() hat die Lösung von (17.21) mit Anfang
hat die Lösung von (17.21) mit Anfang ![]() zur Zeit t=0 die Darstellung
zur Zeit t=0 die Darstellung ![]() , wobei r(t,r0) und
, wobei r(t,r0) und ![]() die Lösung von (17.9a) in Polarkoordinaten ist. Damit ist
die Lösung von (17.9a) in Polarkoordinaten ist. Damit ist
