Definition der topologischen Äquivalenz

Gegeben sei neben (17.1) mit dem zugehörigen Fluß eine weitere autonome Differentialgleichung

wobei eine auf der offenen Menge gegebene C^r-Abbildung ist. Der Fluß von (17.22) möge ebenfalls existieren.

Die Differentialgleichungen (17.1) und (17.22) (bzw. deren Flüsse) heißen topologisch äquivalent, wenn es einen Homöomorphismus (d.h., h ist bijektiv, h und h^-1 sind stetig) gibt, der die Orbits von (17.1) in Orbits von (17.22) unter Beibehaltung der Orientierung, aber nicht unbedingt der Parametrisierung überführt. Die Systeme (17.1) und (17.22) sind also topologisch äquivalent, wenn es neben dem Homöomorphismus eine stetige Abbildung gibt, die bei jedem fixierten streng monoton wachsend ist, auf abbildet, für die für alle ist und die der Beziehung für alle und genügt.

Bei topologischer Äquivalenz gehen Ruhelagen von (17.1) in Ruhelagen von (17.22) und periodische Orbits von (17.1) in periodische Orbits von (17.22) über, wobei die Perioden nicht unbedingt übereinstimmen. Sind also zwei Systeme (17.1) und (17.22) topologisch äquivalent, so stimmt die topologische Struktur der Zerlegung des Phasenraumes in Orbits überein. Sind zwei Systeme (17.1) und (17.22) topologisch äquivalent über den Homöomorphismus und erhält h sogar die Parametrisierung, d.h. gilt so heißen (17.1) und (17.22) topologisch konjugiert.

Topologische Äquivalenz bzw. Konjugiertheit kann sich auch auf Teilmengen der Phasenräume M und N beziehen. Ist z.B. (17.1) auf und (17.22) auf definiert, so heißt (17.1) auf U₁ topologisch äquivalent zu (17.22) auf U₂, wenn ein Homöomorphismus existiert, der die Schnitte der Orbits von (17.1) mit U₁ in Schnitte der Orbits von (17.22) mit U₂ unter Beibehaltung der Orientierung überführt.

Beispiel A

Homöomorphismen für (17.1) und (17.22) sind Abbildungen, bei denen z.B. Strecken und Stauchen der Orbits erlaubt ist, Aufschneiden und Schließen der Orbits dagegen nicht. Die zu den Phasenporträts der folgenden linken und mittleren Abbildung gehörenden Flüsse sind topologisch äquivalent; die zur linken und rechten Abbildung gehörenden Flüsse dagegen nicht.

Beispiel B

Gegeben seien die beiden linearen ebenen Differentialgleichungen (s. [17.19])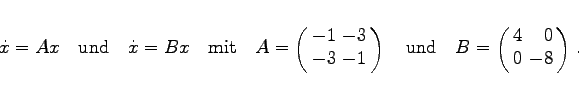

Die Phasenporträts dieser Systeme nahe (0,0) sind in der folgenden linken und rechten Abbildung zu sehen.

Der Homöomorphismus mit , wobei ist, und die Funktion mit überführen die Orbits des ersten Systems in Orbits des zweiten Systems, so daß eine topologische Äquivalenz vorliegt.