Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Gewöhnliche Differentialgleichungen und Abbildungen Strukturelle Stabilität (Robustheit) Strukturstabile Differentialgleichungen
Dynamische Systeme und Chaos Gewöhnliche Differentialgleichungen und Abbildungen Strukturelle Stabilität (Robustheit) Strukturstabile Differentialgleichungen
Die Differentialgleichung (17.1), d.h. das Vektorfeld ![]() , heißt strukturstabil (oder robust), wenn bei kleinen Störungen von f topologisch äquivalente Differentialgleichungen entstehen. Die präzise Definition der Strukturstabilität erfordert einen Abstandsbegriff zwischen zwei Vektorfeldern auf
, heißt strukturstabil (oder robust), wenn bei kleinen Störungen von f topologisch äquivalente Differentialgleichungen entstehen. Die präzise Definition der Strukturstabilität erfordert einen Abstandsbegriff zwischen zwei Vektorfeldern auf ![]() . Wir beschränken uns auf die Betrachtung solcher glatter Vektorfelder auf
. Wir beschränken uns auf die Betrachtung solcher glatter Vektorfelder auf ![]() , die alle eine feste offene, beschränkte und zusammenhängende Menge
, die alle eine feste offene, beschränkte und zusammenhängende Menge ![]() als absorbierende Menge besitzen. Der Rand
als absorbierende Menge besitzen. Der Rand ![]() von U sei eine glatte (n-1)-dimensionale Hyperfläche und sei darstellbar als
von U sei eine glatte (n-1)-dimensionale Hyperfläche und sei darstellbar als ![]() , wobei
, wobei ![]() eine C1-Funktion mit
eine C1-Funktion mit ![]() in einer Umgebung von
in einer Umgebung von ![]() ist. Sei
ist. Sei ![]() der metrische Raum aller glatten Vektorfelder auf
der metrische Raum aller glatten Vektorfelder auf ![]() , versehen mit der C1-Metrik
, versehen mit der C1-Metrik
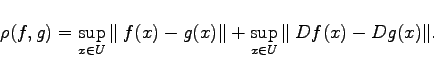 |
(17.25) |
(Im ersten Term der rechten Seite bedeutet ![]() die EUKLIDische Vektornorm, im zweiten die Operatornorm.) Diejenigen glatten Vektorfelder
die EUKLIDische Vektornorm, im zweiten die Operatornorm.) Diejenigen glatten Vektorfelder ![]() , die transversal den Rand
, die transversal den Rand ![]() in Richtung U schneiden, d.h., für die
in Richtung U schneiden, d.h., für die ![]() und
und ![]() gilt, bilden die Menge
gilt, bilden die Menge ![]() . Das Vektorfeld
. Das Vektorfeld ![]() heißt strukturstabil, wenn es ein
heißt strukturstabil, wenn es ein ![]() gibt, so daß jedes andere Vektorfeld
gibt, so daß jedes andere Vektorfeld ![]() mit
mit ![]() topologisch äquivalent zu f ist.
topologisch äquivalent zu f ist.
| Beispiel |
|
Betrachtet wird die ebene Differentialgleichung |
mit einem Parameter ![]() , wobei
, wobei ![]() sei. Die Differentialgleichung g gehört z.B. zu
sei. Die Differentialgleichung g gehört z.B. zu ![]() mit
mit ![]() (s. linke Abbildung). Offenbar gilt
(s. linke Abbildung). Offenbar gilt ![]() . Das Vektorfeld
. Das Vektorfeld ![]() ist strukturell instabil, da beliebig nahe von
ist strukturell instabil, da beliebig nahe von ![]() Vektorfelder existieren, die topologisch nicht äquivalent zu
Vektorfelder existieren, die topologisch nicht äquivalent zu ![]() sind (s. mittlere und rechte Abbildung).
sind (s. mittlere und rechte Abbildung).
Dies wird klar, wenn man zur Polarkoordinatendarstellung ![]() von (17.26) übergeht. Für
von (17.26) übergeht. Für ![]() existiert immer der stabile Grenzzyklus
existiert immer der stabile Grenzzyklus ![]() .
.