Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Dimensionen Auf invariante Maße zurückgehende Dimensionen
Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Dimensionen Auf invariante Maße zurückgehende Dimensionen
Sei ![]() ein Wahrscheinlichkeitsmaß in
ein Wahrscheinlichkeitsmaß in ![]() konzentriert auf
konzentriert auf ![]() . Ist
. Ist ![]() ein beliebiger Punkt,
ein beliebiger Punkt, ![]() die Kugel mit Radius
die Kugel mit Radius ![]() und Mittelpunkt x, so bezeichnen
und Mittelpunkt x, so bezeichnen
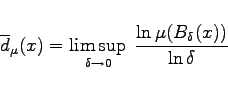 |
(17.42a) |
die obere und
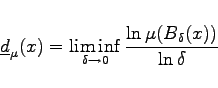 |
(17.42b) |
die untere punktweise Dimension.
Ist ![]() , so heißt
, so heißt ![]() Dimension des Maßes
Dimension des Maßes ![]() in
in ![]() .
.
Satz I von Young: Gilt für ![]() fast alle
fast alle ![]() die Beziehung
die Beziehung ![]() , so ist
, so ist
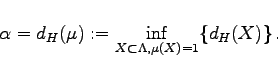 |
(17.43) |
Die Größe ![]() heißt HAUSDORFF-Dimension des Maßes
heißt HAUSDORFF-Dimension des Maßes ![]() .
.
| Beispiel |
|
Es sei |