Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Dimensionen Auf invariante Maße zurückgehende Dimensionen
Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Dimensionen Auf invariante Maße zurückgehende Dimensionen
Der Attraktor ![]() von
von ![]() sei wie bei der Einführung der metrischen Entropie mit Würfeln
sei wie bei der Einführung der metrischen Entropie mit Würfeln ![]() der Seitenlänge
der Seitenlänge ![]() überdeckt. Sei
überdeckt. Sei ![]() ein invariantes Wahrscheinlichkeitsmaß auf
ein invariantes Wahrscheinlichkeitsmaß auf ![]() .
.
Die Entropie der Zerlegung ![]() ist
ist
 |
(17.44) |
gesetzt wurde. Existiert der Grenzwert  , so hat diese Größe die Eigenschaft einer Dimension und wird Informationsdimension genannt.
, so hat diese Größe die Eigenschaft einer Dimension und wird Informationsdimension genannt.
Satz II von Young: Gilt für ![]() -fast alle
-fast alle ![]() die Beziehung
die Beziehung ![]() , so ist
, so ist
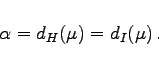 |
(17.45) |
| Beispiel A |
|
Das Maß |
| Beispiel B |
|
Das Maß |