Aufgabenstellung und Lösungsprinzip

Das Verfahren von WOLFE ist zur Lösung von quadratischen Problemen der folgenden speziellen Form geeignet:

Für die hier beschriebene Version des Verfahrens wird als positiv definit vorausgesetzt. Die Grundidee besteht in der Ermittlung einer Lösung des dem Problem (18.55) zugeordneten Systems der KUHN-TUCKER-Bedingungen:

= (18.56a)

= (18.56b) (18.56c)

Die Formeln (18.56a,b,c) stellen ein lineares Gleichungssystem mit m + n Gleichungen und 2n + m nicht negativen Variablen dar. Auf Grund der Bedingung (18.57) muß entweder oder gelten. Daher besitzt jede Lösung von (18.56a,b,c,18.57) höchstens m + n von Null verschiedene Komponenten und muß folglich eine Basislösung von (18.56a,b,c) sein.
Lösungsgang: Mit Hilfe des Simplexverfahrens wird zunächst eine zulässige Basislösung (Ecke) des Systems bestimmt. Die zu den Basisvariablen von gehörenden Indizes bilden die Indexmenge . Um eine Lösung des Systems (18.56a,b,c) zu finden, die auch (18.57) erfüllt, formuliert man das folgende Hilfsproblem:

= (18.59a)

= (18.59b) (18.59c)

Für eine Lösung dieses Problems, die gleichzeitig (18.56a,b,c) und (18.57) erfüllt, muß gelten.
Als zulässige Basislösung für das System (18.59a,b,c) ist bekannt, die gleichzeitig der Bedingung (18.60) genügt. Eine zu dieser Basislösung gehörende Basis wird aus den folgenden Spalten der Koeffizientenmatrix

zusammengesetzt. In (18.61) bedeuten Einheitsmatrix, Nullmatrix und Nullvektor entsprechender Dimension.

1. m Spalten, die zu x_i mit gehören,
2. n - m Spalten, die zu v_i mit gehören,
3. alle m Spalten zu u_i,
4. die letzte Spalte, dafür wird aber eine geeignete der unter b) und c) bestimmten Spalten wieder weggelassen.

Ist , dann ist zwar der Austausch nach d) nicht möglich, es ist dann aber bereits ein Lösungspunkt.

Man kann nunmehr ein erstes Simplextableau aufstellen. Die Minimierung der Zielfunktion erfolgt mit dem Simplexverfahren unter der folgenden Zusatzregel, die sichert:
Bleibt in einem Austauschschritt Basisvariable, dann darf v_i nicht Basisvariable werden und umgekehrt.
Für positiv definites führt das Simplexverfahren unter Beachtung der Zusatzregel zu einer Lösung des Problems (18.58,18.59a,b,c, 18.60) mit . Für positiv semidefinites kann auf Grund der eingeschränkten Pivotelementwahl der Fall eintreten, daß kein Austauschschritt mehr ausgeführt werden kann, ohne die Zusatzregel zu verletzen, obwohl gilt. Man kann zeigen, daß in diesem Fall überhaupt nicht verkleinert werden kann.

Beispiel

In diesem Falle ist lediglich positiv semidefinit. Eine zulässige Basislösung von ist , . Als Basisvektoren werden gewählt:
a) die Spalten 3 und 4 von ,      b) die Spalten 1 und 2 von , c) die Spalten von     und d) die Spalte anstelle der 1. Spalte von .
Aus diesen Spalten wird die Basismatrix gebildet und die Basisinverse errechnet. Durch Multiplikation mit der Matrix (18.61) sowie des Vektors mit der Basisinversen ergibt sich ein erstes Simplextableau:

Schema 9

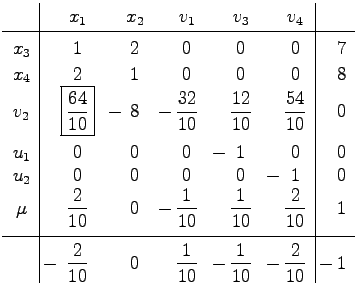Auf Grund der Zusatzregel kann in diesem Tableau nur x₁ gegen v₂ ausgetauscht werden. Als Lösung erhält man nach einigen Austauschschritten . Die letzten zwei Gleichungen von lauten: . Man kann deshalb den Umfang des Problems zu Beginn der Rechnung reduzieren, indem man die freien Variablen u₁ und u₂ aus dem System eliminiert.