Kurvenanpassung und Interpolationsverfahren

1. Kurvenanpassung

Mit Hilfe der Methode der kleinsten Quadrate (s. auch Abschnitt Approximation im Mittel, Diskrete Aufgabe ) kann Mathematica die Anpassung von ausgewählten Funktionen an einen Datensatz durchführen. Die allgemeine Anweisung dafür lautet:

Dabei bilden die y_i die Liste der Daten, funkt ist die Liste der ausgewählten Funktionen, die die Anpassung bewerkstelligen sollen, und x steht für den zugehörigen Wertebereich der unabhängigen Variablen. Wählt man funkt z.B. als , so wird die Anpassung durch ein Polynom n-ten Grades durchgeführt.

Beispiel

Es sei die folgende Liste von Daten gegeben:

0.0302744, 0.0212794}

Mit der Eingabe

wird angenommen, daß den Elementen von l die Werte von x zugeordnet sind. Man erhält das folgende Approximationspolynom 4. Grades:

Mit dem Aufruf

erhält man eine Darstellung der Daten und der Approximationskurve (s. Abbildung).

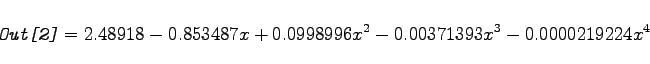
Für die gegebenen Daten ist diese völlig ausreichend. Sie ergeben sich aus den ersten vier Gliedern der Reihenentwicklung von .

2. Interpolation

Mathematica stellt spezielle Algorithmen für die Bestimmung von Interpolationsfunktionen zur Verfügung. Diese werden als sogenannte Objekte dargestellt, die ähnlich wie reine Funktionen aufgebaut sind. Folgende Anweisungen sind vorhanden:

Tabelle Anweisungen zur Interpolation

	erstellt eine Näherungsfunktion mit den Werten yi für die jeweiligen xi=i als ganze Zahlen
	erstellt eine Näherungsfunktion für die Punktfolge (xi,yi)

Anstelle der Funktionswerte y_i kann eine Liste aus Funktionswert und spezifizierten Ableitungen an der jeweiligen Stelle eingegeben werden.

Beispiel

Mit erhält man die folgende Abbildung:

Man erkennt, daß Mathematica eine präzise Nachbildung der Datenliste liefert.