Orthogonalisierungsverfahren

Grundlage der folgenden Orthogonalisierungsverfahren zur Lösung der linearen Ausgleichsaufgabe (19.40) sind die folgenden Aussagen:

1. Die Länge eines Vektors bleibt unter orthogonalen Transformationen invariant, d.h., die Vektoren und mit einer orthogonalen Matrix , d.h. mit

   haben dieselbe Länge.

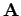
2. Zu jeder Matrix vom Typ (m,n) mit Maximalrang existiert eine orthogonale Matrix vom Typ , so daß gilt:

   mit

Dabei ist eine Rechtsdreiecksmatrix vom Typ , und ist eine Nullmatrix vom Typ . Die Faktorisierung (19.43) der Matrix heißt QR-Zerlegung. Damit können die Fehlergleichungen (19.39) in das äquivalente System

überführt werden, ohne daß dabei die Summe der Quadrate der Residuen verändert wird. Aus (19.46) folgt, daß diese Quadratsumme für minimal wird und der Minimalwert gleich der Summe der Quadrate von bis ist. Die gesuchte Lösung erhält man durch Rückwärtseinsetzen aus

wobei der Vektor ist, der aus den Werten aus (19.46) gebildet wird.
Zur schrittweisen Überführung von (19.39) in (19.46) werden vor allem zwei Methoden verwendet:

1. GIVENS-Transformation,
2. HOUSEHOLDER-Transformation.

Die erste erzeugt eine QR-Zerlegung der Matrix durch Drehungen, die zweite durch Spiegelungen. Die numerischen Realisierungen findet man in [19.29].
Praktische Aufgaben der linearen Quadratmittelapproximation werden vorwiegend mit der HOUSEHOLDER-Transformation gelöst, wobei man in vielen Fällen noch die spezielle Struktur der Koeffizientenmatrix 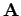wie Bandstruktur oder schwache Besetztheit ausnutzen kann.