Inhalt Index DeskTop Bronstein
![]()
![]() Numerische Mathematik Numerische Lösung von Gleichungssystemen Nichtlineare Gleichungssysteme
Numerische Mathematik Numerische Lösung von Gleichungssystemen Nichtlineare Gleichungssysteme
Das gewöhnliche Iterationsverfahren geht davon aus, daß sich die Gleichungen (19.55) auf eine Fixpunktform
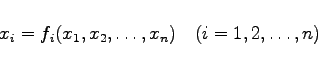 |
(19.56) |
bringen lassen. Dann erhält man, von den geschätzten Näherungswerten ![]() ausgehend, verbesserte Werte durch
ausgehend, verbesserte Werte durch
| = |  |
||
| (19.57) |
| = | 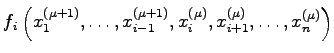 |
||
| (19.58) |
Für die Güte der Konvergenz dieser Verfahren ist ausschlaggebend, daß die Funktionen fi in der Umgebung einer Lösung möglichst schwach von den Unbekannten abhängen, d.h., falls die fi differenzierbar sind, müssen die Beträge der partiellen Ableitungen möglichst klein sein. Als Konvergenzbedingung erhält man
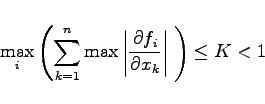 |
(19.59) |
auf einer Umgebung der anzunähernden Lösung. Mit einer solchen Größe K gilt die Fehlerabschätzung
Dabei sind xi die Komponenten der gesuchten Lösung, ![]() und
und ![]() die zugehörigen
die zugehörigen ![]() -ten und
-ten und ![]() -ten Näherungen.
-ten Näherungen.