Inhalt Index DeskTop Bronstein
![]()
![]() Numerische Mathematik Numerische Lösung von Gleichungssystemen Nichtlineare Gleichungssysteme
Numerische Mathematik Numerische Lösung von Gleichungssystemen Nichtlineare Gleichungssysteme
Das NEWTON-Verfahren geht von der Nullstellenaufgabe (19.55) aus. Nach Vorgabe von geschätzten Näherungswerten ![]() werden die Funktionen Fi als Funktionen von n unabhängigen Variablen
werden die Funktionen Fi als Funktionen von n unabhängigen Variablen ![]() nach TAYLOR entwickelt. Durch Abbruch dieser Entwicklungen nach den linearen Gliedern erhält man aus (19.55) ein lineares Gleichungssystem, mit dessen Hilfe man iterativ Verbesserungen nach folgender Vorschrift ermitteln kann:
nach TAYLOR entwickelt. Durch Abbruch dieser Entwicklungen nach den linearen Gliedern erhält man aus (19.55) ein lineares Gleichungssystem, mit dessen Hilfe man iterativ Verbesserungen nach folgender Vorschrift ermitteln kann:
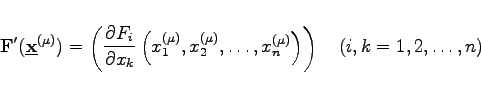 |
(19.62) |
und wird als JACOBI-Matrix bezeichnet. Das NEWTON-Verfahren ist lokal quadratisch konvergent; seine schnelle Konvergenz ist wesentlich von der Güte der Startnäherungen abhängig. Setzt man in (19.61) ![]() , dann kann das NEWTON-Verfahren in der Korrekturform
, dann kann das NEWTON-Verfahren in der Korrekturform
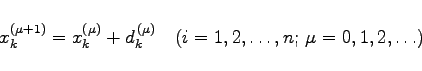 |
(19.63) |
geschrieben werden. Zur Herabsetzung der Startwertempfindlichkeit kann man dann analog zum Relaxationsverfahren einen sogenannten Dämpfungs- oder Schrittweitenparameter ![]() einführen:
einführen:
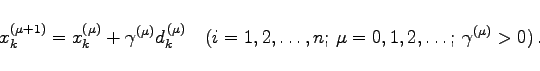 |
(19.64) |
Angaben zur Bestimmung von ![]() findet man in [19.31].
findet man in [19.31].