Inhalt Index DeskTop Bronstein
![]()
![]() Numerische Mathematik Numerische Integration Interpolationsquadraturen
Numerische Mathematik Numerische Integration Interpolationsquadraturen
Im Intervall [x0,x0+h] wird f(x) durch ein Polynom 1. Grades ersetzt, das f(x) an den Stützstellen x0 und x1 = x0+h interpoliert. Man erhält:
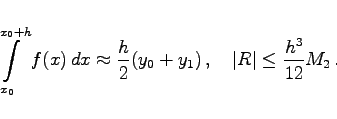 |
(19.75) |
Durch Summation ergibt sich die sogenannte zusammengesetzte Trapezformel oder Trapezsumme:
Mit M2 wird eine für den gesamten Bereich der Stützstellen gültige obere Schranke für | f''(x) | bezeichnet.
Der Fehler der Trapezsumme verhält sich wie ![]() , d.h., die Trapezsumme hat die Fehlerordnung 2. Daraus folgt für
, d.h., die Trapezsumme hat die Fehlerordnung 2. Daraus folgt für ![]() (also
(also ![]() ) ihre Konvergenz gegen das bestimmte Integral, wenn Rundungsfehler nicht berücksichtigt werden.
) ihre Konvergenz gegen das bestimmte Integral, wenn Rundungsfehler nicht berücksichtigt werden.