CASSINIsche Kurven nennt man den geometrischen Ort aller Punkte P, für die das Produkt der Abstände von zwei festen Punkten F1 und F2 bei (c,0) bzw.  , den Fixpunkten, konstant gleich a2 ist:
, den Fixpunkten, konstant gleich a2 ist:
 |
(2.227) |
Die Gleichung lautet in kartesischen und Polarkoordinaten:
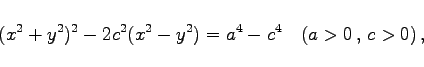 |
(2.228a) |
 |
(2.228b) |
Die Form der Kurve hängt von den Größen a und c ab:

- 1. Fall

- Für
 ist die Kurve ein ellipsenförmiges Oval.
ist die Kurve ein ellipsenförmiges Oval.
Die Schnittpunkte A und C mit der x-Achse liegen bei  , die Schnittpunkte B und D mit der y-Achse bei
, die Schnittpunkte B und D mit der y-Achse bei 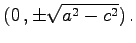
- 2. Fall
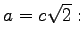
- Für den Fall
 ergibt sich eine Kurve des gleichen Typs mit A und C bei
ergibt sich eine Kurve des gleichen Typs mit A und C bei  und B und D bei
und B und D bei  wobei die Krümmung in den Punkten B und D gleich 0 ist, d.h., es gibt eine enge Berührung mit den Geraden
wobei die Krümmung in den Punkten B und D gleich 0 ist, d.h., es gibt eine enge Berührung mit den Geraden 
- 3. Fall
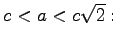
- Für
 ist die Kurve ein eingedrücktes Oval.
ist die Kurve ein eingedrücktes Oval.
Die Achsenschnitte sind dieselben wie im Falle  ebenso das Maximum und das Minimum B, D, während die weiteren Extrema E, G, K, I bei
ebenso das Maximum und das Minimum B, D, während die weiteren Extrema E, G, K, I bei  liegen und die vier Wendepunkte P, L, M, N bei
liegen und die vier Wendepunkte P, L, M, N bei  mit
mit  und
und 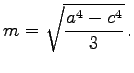
- 4. Fall a = c:
- Für a = c ergibt sich die Lemniskate.
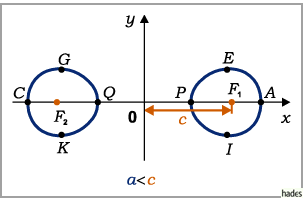
- 5. Fall a < c:
- Für a < c ergeben sich zwei Ovale.
Die Schnittpunkte A und C mit der x-Achse liegen bei  die Schnittpunkte P und Q bei
die Schnittpunkte P und Q bei  die Maxima und Minima E, G, K, I bei
die Maxima und Minima E, G, K, I bei 
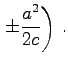
Der Krümmungsradius beträgt  wobei
wobei  der Polarkoordinatendarstellung genügt.
der Polarkoordinatendarstellung genügt.
![]() , den Fixpunkten, konstant gleich a2 ist:
, den Fixpunkten, konstant gleich a2 ist:
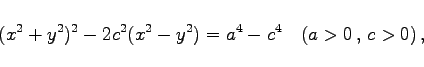

 liegen und die vier Wendepunkte P, L, M, N bei
liegen und die vier Wendepunkte P, L, M, N bei  mit
mit  und
und 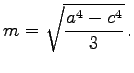

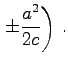
 wobei
wobei