Epizykloide wird eine Kurve genannt, die von einem Peripheriepunkt eines Kreises beschrieben wird, wenn dieser, ohne zu gleiten, auf der Außenseite eines anderen Kreises abrollt.
Die Gleichung der Epizykloide lautet in Parameterform mit A als Radius des festen und a als Radius des rollenden Kreises
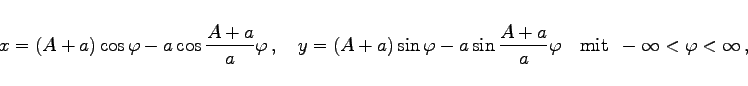 |
(2.233) |
wobei ![]() gilt. Die Form der Kurve hängt vom Quotienten
gilt. Die Form der Kurve hängt vom Quotienten 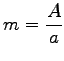 ab.
ab.
Für m = 1 erhält man die Kardioide.
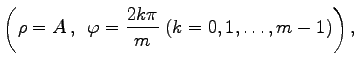 die Scheitelpunkte
die Scheitelpunkte 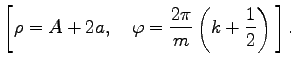
Die Länge eines Zweiges beträgt  Bei ganzzahligem m ist die Länge der gesamten Kurve
Bei ganzzahligem m ist die Länge der gesamten Kurve ![]()
Die Fläche des Sektors A1B1A2A1 beträgt (ohne den Sektor des festen Kreises) 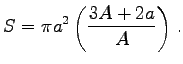
Der Krümmungsradius ist 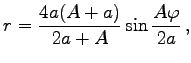 in den Scheiteln
in den Scheiteln 