Eigenwerte und Eigenvektoren

In Abschnitt Eigenwertaufgaben bei Matrizen sind Eigenwerte und Eigenvektoren von Matrizen definiert worden. Mathematica bietet die Möglichkeit, diese mit speziellen Anweisungen zu bestimmen. So liefert eine Liste der Eigenvektoren der quadratischen Matrix eine Liste der Eigenvektoren von m. Setzt man anstelle von m aber , so erhält man die numerischen Eigenwerte. Bei Matrizen mit der Ordnung n > 4 kann man im allgemeinen keine algebraischen Ausdrücke mehr erwarten, da die zu lösende Polynomgleichung höher als vierten Grades ist. Deshalb kann man in diesen Fällen nur nach numerischen Werten fragen.

Beispiel

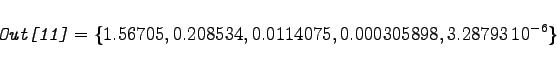Das erzeugt eine 5-dimensionale sogenannte HILBERT-Matrix.

Mit der Anweisung

antwortet Mathematica

Gibt man aber ein

so erhält man