Lösung linearer Gleichungssysteme

Zur Behandlung linearer Gleichungssysteme stellt Maple spezielle Operationen bereit, die im Paket für linare Algebra enthalten sind. Speziell handelt es sich um . Das lineare Gleichungssystem liegt in der Form

vor, wobei A seine Matrix bezeichnet und c den Vektor der rechten Seite des Gleichungssystems.

Besitzt das System keine Lösung, dann wird die Null-Sequenz zurückgegeben. Hat das System mehrere linear unabhängige Lösungen, so werden diese in Parameterdarstellung wiedergegeben.

Die Operation findet eine Basis im Nullraum der Matrix A, der für eine singuläre Matrix von Null verschieden ist.

Für die Lösung von Gleichungssystemen können auch die Operationen der Matrixmultiplikation und die Bestimmung von inversen Matrizen benutzt werden.

Beispiel A

Es wird das Beispiel aus Abschnitt Triviale Lösung und Fundamentalsystem des homogenen Systems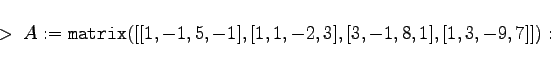

betrachtet, dessen Matrix singulär ist. Das dort untersuchte homogene System besitzt nichttriviale Lösungen. Zur Lösung wird zunächst die Matrix A definiert:

Mit kann man sich überzeugen, daß sie singulär ist, und über

kann die Liste zweier linear unabhängiger Vektoren bestimmt werden. Diese Vektoren bilden eine Basis im zweidimensionalen Nullraum der Matrix A.

Für den allgemeinen Fall stellt Maple Operationen zur Anwendung des GAUSSschen Algorithmus zur Verfügung, die in der folgenden Tabelle aufgeführt sind.

Tabelle Operationen des GAUSSschen Algorithmus

	erzeugt aus A durch Addition von Vielfachen der i-ten Zeile zu allen anderen Zeilen eine Matrix, deren j-te Spalte außer Aij aus Nullen besteht
	erzeugt die durch Zeilenpivotisierung entstehende GAUSSsche Dreiecksmatrix. Die Matrixelemente müssen rationale Zahlen sein
	erzeugt eine Diagonalmatrix nach dem GAUSS-JORDAN-Verfahren, die Matrixelemente können Gleitpunktzahlen sein
	erzeugt die Matrix, die durch Anfügen einer Spalte (gegeben durch den Vektor u) aus A entsteht

Hat man ein Gleichungssystem mit gleicher Anzahl von Gleichungen und Unbekannten sowie nichtsingulärer Matrix, so löst man das System mit .

Beispiel B

Es soll das System aus Kapitel Numerische Mathematik, Abschnitt GAUSS-SEIDEL-Verfahren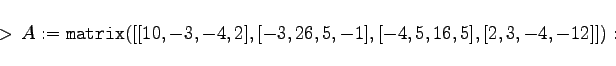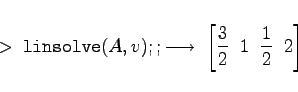

gelöst werden. Hier ist

Mit linsolve erhält man

Der GAUSS-Algorithmus wird mit

angewendet.

Beispiel C

Es soll das inhomogene Gleichungssystem des Beispiels B aus Abschnitt Allgemeine Regel für das inhomogene System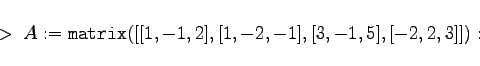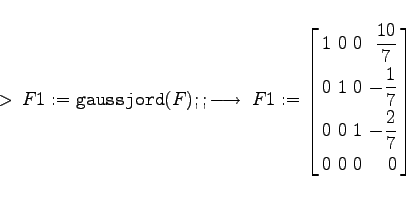

gelöst werden. Dazu werden zunächst die zugehörige Matrix und der Vektor der rechten Seite definiert:

Das System ist überbestimmt. Um es zu lösen, kann linsolve nicht benutzt werden. Daher bestimmt man

Mit gaussjord kann die Matrix F in eine obere Dreiecksform gebracht werden:

Der Lösungsvektor ist unmittelbar aus F1 ablesbar.