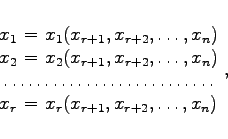Besitzt es eine nichttriviale Lösung


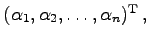
d.h.
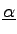
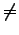

, dann ist auch
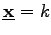
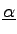
mit
k beliebig reell eine Lösung des homogenen Gleichungssystems. Besitzt es
l nichttriviale, linear unabhängige Lösungen
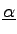

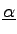

...,
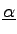
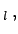
dann bilden diese ein sogenanntes
Fundamentalsystem, und die allgemeine Lösung des homogenen linearen Gleichungssystems ist von der Form
 |
(4.109) |
Gilt für den Rang der Koeffizientenmatrix  des homogenen Gleichungssystems r < n, wobei n die Anzahl der Unbekannten ist, dann besitzt das homogene Gleichungssystem ein Fundamentalsystem von Lösungen. Im Falle r = n hat das homogene System nur die Triviallösung.
des homogenen Gleichungssystems r < n, wobei n die Anzahl der Unbekannten ist, dann besitzt das homogene Gleichungssystem ein Fundamentalsystem von Lösungen. Im Falle r = n hat das homogene System nur die Triviallösung.
Zur Bestimmung eines Fundamentalsystems im Falle r < n können n - r Unbekannte als freie Parameter gewählt werden, und zwar derart, daß sich die übrigen Unbekannten durch diese ausdrücken lassen, d.h., die entsprechende r-reihige Unterdeterminante darf nicht Null sein. Man kann das durch Umordnen der Gleichungen und Unbekannten erreichen. Erhält man z.B.
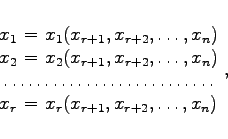 |
(4.110) |
dann ergeben sich die Fundamentallösungen z.B. durch die folgende Wahl der freien Parameter:
 |
(4.111) |
![]()
![]() Lineare Algebra Lineare Gleichungssysteme Lösung linearer Gleichungssysteme Definition und Lösbarkeit
Lineare Algebra Lineare Gleichungssysteme Lösung linearer Gleichungssysteme Definition und Lösbarkeit
![]() existiert, der (4.107a) zu einer Identität macht. Anderenfalls heißt das System unlösbar.
existiert, der (4.107a) zu einer Identität macht. Anderenfalls heißt das System unlösbar.![]() ab, die durch Hinzufügen der Komponenten des Vektors
ab, die durch Hinzufügen der Komponenten des Vektors ![]() als (n + 1)-te Spalte zur Matrix
als (n + 1)-te Spalte zur Matrix ![]() entsteht.
entsteht.
![]() gilt die folgende Fallunterscheidung:
gilt die folgende Fallunterscheidung:


![]() des homogenen Gleichungssystems r < n, wobei n die Anzahl der Unbekannten ist, dann besitzt das homogene Gleichungssystem ein Fundamentalsystem von Lösungen. Im Falle r = n hat das homogene System nur die Triviallösung.
des homogenen Gleichungssystems r < n, wobei n die Anzahl der Unbekannten ist, dann besitzt das homogene Gleichungssystem ein Fundamentalsystem von Lösungen. Im Falle r = n hat das homogene System nur die Triviallösung.