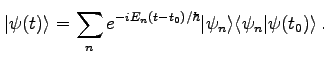Lösung der Schrödinger-Gleichung als Eigenwertproblem
Wenn der HAMILTON-Operator  nicht von der Zeit abhängt, so gilt:
nicht von der Zeit abhängt, so gilt:
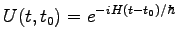 |
(21.83) |
Die Lösung der Schrödinger-Gleichung ist in diesem Fall äquivalent zur Diagonalisierung von  , also der Berechnung aller Eigenwerte
, also der Berechnung aller Eigenwerte  und aller dazugehörigen Eigenvektoren
und aller dazugehörigen Eigenvektoren  von
von  :
:
 |
(21.84) |
Gleichung 21.84 wird auch als stationäre SCHRÖDINGER-Gleichung bezeichnet. Für einen beliebigen Zustandsvektor  zum Zeitpunkt
zum Zeitpunkt  lautet dann die Lösung zum Zeitpunkt
lautet dann die Lösung zum Zeitpunkt  :
:
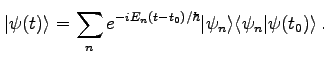 |
(21.85) |
![]()
![]() Mathematische Grundlagen der Quantenmechanik Physikalische Postulate Zeitentwicklung
Mathematische Grundlagen der Quantenmechanik Physikalische Postulate Zeitentwicklung
![]() nicht von der Zeit abhängt, so gilt:
nicht von der Zeit abhängt, so gilt: