Beispiele für Lösungen der Schrödinger-Gleichung

Für ein Teilchen der Masse , das sich in einem Potential bewegt, gilt der HAMILTON-Operator 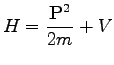bzw. in Ortsdarstellung 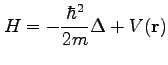, mit dem LAPLACE-Operator .

Die stationäre SCHRÖDINGER-Gleichung 21.84 stellt sich deshalb als eine im allgemeinen gekoppelte partielle Differentialgleichung dar, für eindimensionale Probleme vereinfacht sie sich jedoch zu einer gewöhnlichen Differentialgleichung (siehe SCHRÖDINGER-Gleichung).

Beispiel A: Freies Teilchen in einer Dimension

Potential

DGL

Lösung

ebene Wellen mit . Alle Energien sind erlaubt.

Hinweis Man beachte, daß eine ebene Welle keine Norm hat () und somit kein Vektor im HILBERT-Raum ist. Dieses für Eigenzustände von Operatoren mit kontinuierlichem Spektrum typische Problem läßt sich durch entsprechende Erweiterung des HILBERT-Raumes in den Griff bekommen [23.1].

Beispiel B: Kastenpotential in einer Dimension

Potential

DGL

Wie freies Teilchens für , aber mit Randbedingung .

Lösung

für mit und . ist eine Konstante zur Normierung der Wellenfunktion. Nur diskrete Energien sind erlaubt.Außerhalb gilt .

In der Abbildung sind die Eigenfunktionen für die ersten fünf Eigenenergien aufgetragen.

Beispiel C: Kastenpotential in drei Dimensionen

Potential

DGL

innerhalb des Kastens mit Randbedingung für oder oder .

Lösung

mit und , und der Konstanten zur Normierung. Nur diskrete Energien sind erlaubt.

Beispiel D: Harmonischer Oszillator in einer Dimension

Potential

DGL

Lösung

HERMITEsche Funktionen

mit den HERMITEschen Polynomen (siehe Linearer harmonischer Oszillator). Nur Energien mit sind erlaubt.

In der Abbildung sind die hermiteschen Funktionen für die ersten sechs Eigenenergien aufgetragen.