Inhalt Index DeskTop Bronstein
![]()
![]() Geometrie Vektoralgebra und analytische Geometrie Vektoralgebra Definition des Vektors
Geometrie Vektoralgebra und analytische Geometrie Vektoralgebra Definition des Vektors
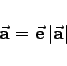 |
(3.260a) |
angegeben werden. Zur Beschreibung der drei Koordinatenachsen in Richtung wachsender Koordinatenwerte werden oft die Einheitsvektoren ![]() oder
oder ![]() verwendet.
verwendet.
In der Abbildung bilden die durch die drei Einheitsvektoren festgelegten Richtungen ein senkrechtes Richtungstripel. Außerdem bilden sie ein orthogonales Koordinatensystem, denn es gilt:
 |
(3.260b) |
Zudem gilt
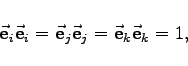 |
(3.260c) |
so daß man von einem orthonormierten Koordinatensystem spricht.
In diesem Falle heißt der Koordinatenursprung Pol. Der Punkt P ist durch seinen Radiusvektor eindeutig bestimmt.