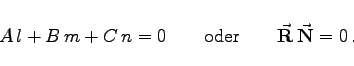Winkel zwischen zwei Geraden
- 1. Allgemeiner Fall:
- Sind die Geraden durch die Gleichungen
 und
und 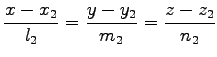 oder vektoriell durch
oder vektoriell durch
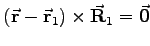 und
und 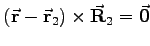 gegeben, dann wird der Winkel gemäß
gegeben, dann wird der Winkel gemäß
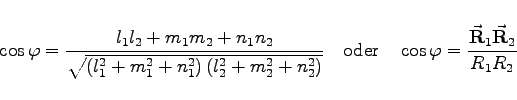 |
(3.426) |
mit  und
und 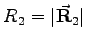 berechnet.
berechnet.
- 2. Parallelitätsbedingung:
- Die Parallelitätsbedingung für zwei Geraden lautet:
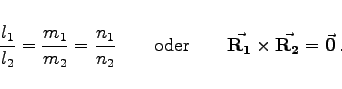 |
(3.427) |
- 3. Orthogonalitätsbedingung:
- Die Orthogonalitätsbedingung für zwei Geraden lautet:
 |
(3.428) |
Winkel zwischen einer Geraden und einer Ebene
- Gleichungen:
- Sind die Gerade und die Ebene gegeben durch die Gleichungen
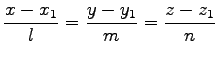 bzw. Ax + By + Cz + D = 0 oder vektoriell durch
bzw. Ax + By + Cz + D = 0 oder vektoriell durch 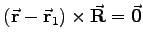 bzw.
bzw. 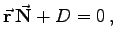 dann wird der Winkel zu
dann wird der Winkel zu
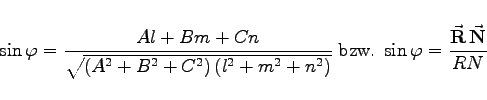 |
(3.429) |
mit 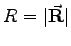 und
und  berechnet.
berechnet.
- Parallelitätsbedingung:
- Die Parallelitätsbedingung für eine Gerade und eine Ebene lautet:
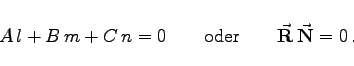 |
(3.430) |
- Orthogonalitätsbedingung:
- Die Ortogonalitätsbedingung für eine Gerade und eine Ebene lautet:
 |
(3.431) |
![]()
![]() Geometrie Vektoralgebra und analytische Geometrie Analytische Geometrie des Raumes Gerade und Ebene im Raum
Geometrie Vektoralgebra und analytische Geometrie Analytische Geometrie des Raumes Gerade und Ebene im Raum
 und
und 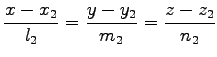 oder vektoriell durch
oder vektoriell durch![]() und
und ![]() berechnet.
berechnet.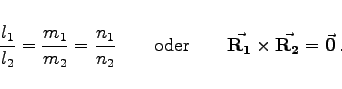

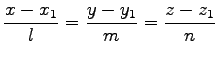 bzw. Ax + By + Cz + D = 0 oder vektoriell durch
bzw. Ax + By + Cz + D = 0 oder vektoriell durch 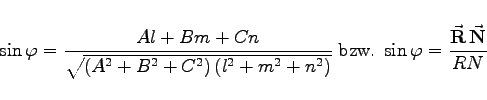
![]() und
und ![]() berechnet.
berechnet.