Inhalt Index DeskTop Bronstein
![]()
![]() Lineare Algebra Eigenwertaufgaben bei Matrizen Spezielles Eigenwertproblem Hauptachsentransformation quadratischer Formen
Lineare Algebra Eigenwertaufgaben bei Matrizen Spezielles Eigenwertproblem Hauptachsentransformation quadratischer Formen
Mit ![]() sei eine beliebige reelle oder komplexe quadratische Matrix vom Typ (n,n) gegeben. Dann gibt es eine nichtsinguläre Matrix
sei eine beliebige reelle oder komplexe quadratische Matrix vom Typ (n,n) gegeben. Dann gibt es eine nichtsinguläre Matrix ![]() , so daß
, so daß
 |
(4.139) |
gilt, wobei J als JORDAN-Matrix oder JORDANsche Normalform von ![]() bezeichnet wird. Die JORDAN-Matrix hat die Gestalt
bezeichnet wird. Die JORDAN-Matrix hat die Gestalt
 |
(4.140) |
wobei die Elemente ![]() von
von ![]() auch als JORDAN-Kästchen bezeichnet werden. Für deren Form gilt:
auch als JORDAN-Kästchen bezeichnet werden. Für deren Form gilt:
1. Sind alle Eigenwerte ![]() von
von ![]() einfach, so ist
einfach, so ist ![]() und
und ![]() , d.h.,
, d.h., ![]() ist eine Diagonalmatrix der Form
ist eine Diagonalmatrix der Form
 |
(4.141) |
2. Ist ![]() ein pj-facher Eigenwert von A, so gibt es ein oder mehrere JORDAN-Kästchen der Form
ein pj-facher Eigenwert von A, so gibt es ein oder mehrere JORDAN-Kästchen der Form
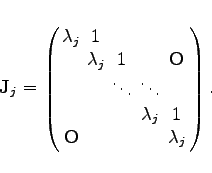 |
(4.142) |
Dabei gilt  . Die Summe der Dimensionen der JORDAN-Kästchen zu einem Eigenwert ist
. Die Summe der Dimensionen der JORDAN-Kästchen zu einem Eigenwert ist ![]() . Weitere Informationen zu den JORDAN-Kästchen findet man in Lit. [[4.18]], [[19.3]] Bd. 1.
. Weitere Informationen zu den JORDAN-Kästchen findet man in Lit. [[4.18]], [[19.3]] Bd. 1.