Inhalt Index DeskTop Bronstein
![]()
![]() Lineare Algebra Quaternionen und Anwendungen Quaternionen Rechenregeln
Lineare Algebra Quaternionen und Anwendungen Quaternionen Rechenregeln
Da die Multiplikation assoziativ ist, gilt
| ( | |||
| = | |||
| + | (4.165) |
wobei ![]() das Skalarprodukt und
das Skalarprodukt und ![]() das Vektorprodukt der Vektoren
das Vektorprodukt der Vektoren ![]() bezeichnet. Anschließend identifiziert man den
bezeichnet. Anschließend identifiziert man den ![]() mit dem Raum
mit dem Raum ![]() der reinen Quaternionen.
der reinen Quaternionen.
Man beachte: Die Multiplikation von Quaternionen ist nicht kommutativ!
Der Viererektor ![]() entspricht der linksseitigen Matrizenmultiplikation der Matrix
entspricht der linksseitigen Matrizenmultiplikation der Matrix ![]() mit dem Vektor
mit dem Vektor ![]() und ist gleich der rechtsseitigen Matrizenmultiplikation der Matrix
und ist gleich der rechtsseitigen Matrizenmultiplikation der Matrix ![]() mit dem Vektor
mit dem Vektor ![]()
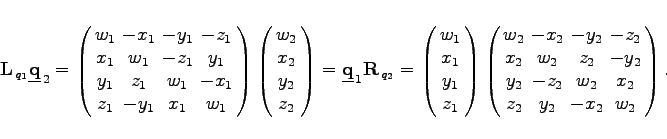 |
(4.167) |