Inhalt Index DeskTop Bronstein
![]()
![]() Lineare Algebra Matrizen Rechenoperationen mit Matrizen Multiplikation zweier Matrizen
Lineare Algebra Matrizen Rechenoperationen mit Matrizen Multiplikation zweier Matrizen
Für zwei Vektoren ![]() und
und ![]() die als einspaltige bzw. einzeilige Matrizen dargestellt werden können, gibt es bei der Matrizenmultiplikation die folgenden zwei Möglichkeiten der Produktbildung:
die als einspaltige bzw. einzeilige Matrizen dargestellt werden können, gibt es bei der Matrizenmultiplikation die folgenden zwei Möglichkeiten der Produktbildung:
Ist ![]() vom Typ (1,n) und
vom Typ (1,n) und ![]() vom Typ (n,1), dann ist das Produkt vom Typ (1,1), also eine Zahl. Man spricht dann vom Skalarprodukt zweier Vektoren.
vom Typ (n,1), dann ist das Produkt vom Typ (1,1), also eine Zahl. Man spricht dann vom Skalarprodukt zweier Vektoren.
Ist dagegen ![]() vom Typ (n,1) und
vom Typ (n,1) und ![]() vom Typ
vom Typ ![]() dann ist das Produkt vom Typ (n,m), also eine Matrix. Man spricht in diesem Falle vom dyadischen Produkt zweier Vektoren.
dann ist das Produkt vom Typ (n,m), also eine Matrix. Man spricht in diesem Falle vom dyadischen Produkt zweier Vektoren.
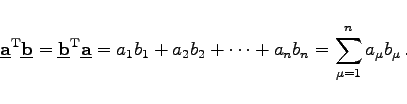 |
(4.24) |
Das Kommutativgesetz der Multiplikation gilt hier im allgemeinen nicht. Daher ist die Reihenfolge von ![]() und
und ![]() exakt einzuhalten. Bei Vertauschung der Reihenfolge, also
exakt einzuhalten. Bei Vertauschung der Reihenfolge, also ![]() würde sich ein dyadisches Produkt ergeben.
würde sich ein dyadisches Produkt ergeben.
 |
(4.25) |
vom Typ (n,m). Auch hier gilt das Kommutativgesetz der Multiplikation im allgemeinen nicht.