Inhalt Index DeskTop Bronstein
Lineare Algebra Tensoren Tensoren in krummlinigen Koordinatensystemen Kovariante, kontravariante und gemischte Koordinaten von Tensoren 2. Stufe
Beim Übergang zu einem neuen Koordinatensystem geht (4.92a) in
 |
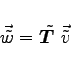(4.93a) |
über. Dabei entsteht zwischen den Komponenten von T und 
der Zusammenhang
Man führt die Bezeichnung
ein und spricht von gemischten Koordinaten des Tensors, weil der Index k für kontravariant, der Index l für kovariant steht. Für die Komponenten der Vektoren 
und 
gilt dann
Ersetzt man die kovariante Basis 
durch die kontravariante Basis 
dann erhält man analog zu (4.93b) und (4.93c)
 |
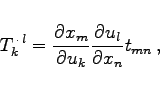(4.94a) |
und (4.93d) geht in
über. Zwischen den gemischten Koordinaten 
und 
besteht der Zusammenhang
 |
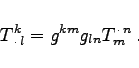(4.94c) |
