Inhalt Index DeskTop Bronstein
![]()
![]() Algebra und Diskrete Mathematik Klassische algebraische Strukturen Anwendungen von Gruppen
Algebra und Diskrete Mathematik Klassische algebraische Strukturen Anwendungen von Gruppen
Zu jeder Symmetrieoperation S gibt es eine inverse Operation ![]() die S wieder rückgängig macht, d.h., es gilt
die S wieder rückgängig macht, d.h., es gilt
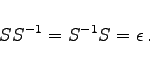 |
(5.178) |
Dabei bezeichnet ![]() die identische Operation, die den gesamten Raum unverändert läßt. Die Gesamtheit der Symmetrieoperationen eines räumlichen Objektes bildet bezüglich der Hintereinander-Ausführung eine Gruppe, die im allgemeinen nichtkommutative Symmetriegruppe des Objektes. Dabei gelten die folgenden Beziehungen:
die identische Operation, die den gesamten Raum unverändert läßt. Die Gesamtheit der Symmetrieoperationen eines räumlichen Objektes bildet bezüglich der Hintereinander-Ausführung eine Gruppe, die im allgemeinen nichtkommutative Symmetriegruppe des Objektes. Dabei gelten die folgenden Beziehungen:
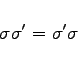 |
(5.179) |
genau dann, wenn die zugehörigen Spiegelungsebenen identisch sind oder senkrecht aufeinander stehen. Im ersten Fall ist das Produkt die Identität ![]() im zweiten die Drehung
im zweiten die Drehung ![]()
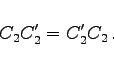 |
(5.180) |
Das Produkt ist jeweils wieder eine Drehung. Im ersten Fall ist die zugehörige Drehachse die gegebene, im zweiten steht die Drehachse senkrecht auf den beiden gegebenen.