Inhalt Index DeskTop Bronstein
![]()
![]() Algebra und Diskrete Mathematik Elementare Zahlentheorie Kongruenzen und Restklassen
Algebra und Diskrete Mathematik Elementare Zahlentheorie Kongruenzen und Restklassen
 |
(5.268) |
Die Restklasse a modulo m besteht aus allen ganzen Zahlen, die bei Division durch m den gleichen Rest wie a lassen. Es gilt [a]m=[b]m genau dann, wenn ![]() mod m ist.
mod m ist.
Zum Modul m gibt es genau m Restklassen, zu deren Beschreibung man in der Regel ihre kleinsten nichtnegativen Repräsentanten verwendet:
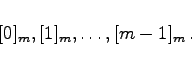 |
(5.269) |
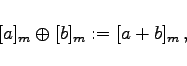 |
(5.270) |
 |
(5.271) |
eine Restklassenaddition bzw.Restklassenmultiplikation erklärt.
Diese Restklassenoperationen sind unabhängig von der Auswahl der Repräsentanten, d.h., aus
 |
(5.272a) |
folgt
 |
(5.272b) |
und
 |
(5.272c) |