Inhalt Index DeskTop Bronstein
![]()
![]() Algebra und Diskrete Mathematik Mengenlehre Mengenbegriff, spezielle Mengen
Algebra und Diskrete Mathematik Mengenlehre Mengenbegriff, spezielle Mengen
| Menge der natürlichen Zahlen, | ||
| Menge der ganzen Zahlen, | ||
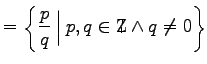 |
Menge der rationalen Zahlen, | |
| Menge der reellen Zahlen, | ||
| Menge der komplexen Zahlen. |
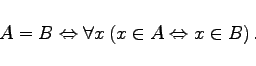 |
(5.35) |
| Beispiel |
|
Die Mengen {3,1,3,7,2} und {1,2,3,7} sind gleich. |