Inhalt Index DeskTop Bronstein
![]()
![]() Algebra und Diskrete Mathematik Mengenlehre Mengenbegriff, spezielle Mengen
Algebra und Diskrete Mathematik Mengenlehre Mengenbegriff, spezielle Mengen
 |
(5.36) |
dann heißt A Teilmenge von B, und man schreibt: ![]() Mit anderen Worten: A ist Teilmenge von
Mit anderen Worten: A ist Teilmenge von ![]() wenn alle Elemente von A auch zu B gehören. Damit gilt auch stets
wenn alle Elemente von A auch zu B gehören. Damit gilt auch stets ![]() .
.
Gibt es für ![]() in B weitere Elemente, die nicht in A vorkommen, so heißt A echte Teilmenge von
in B weitere Elemente, die nicht in A vorkommen, so heißt A echte Teilmenge von ![]() , und man schreibt
, und man schreibt ![]() Die folgende Abbildung zeigt A als echte Teilmenge der Menge
Die folgende Abbildung zeigt A als echte Teilmenge der Menge ![]()
| Beispiel |
|
Es seien A = {2, 4, 6, 8, 10} eine Menge gerader Zahlen und |
| Beispiel A |
|
Die Menge |
| Beispiel B |
|
Für jede Menge M gilt |
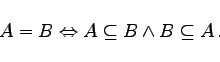 |
(5.37) |
Diese Tatsache wird häufig zum Beweis der Gleichheit zweier Mengen benutzt.
| Beispiel |
|
Für die Menge M={a,b,c,} lautet die Potenzmenge
|