Weitere Mengenoperationen

Außer den in den vorhergehenden Abschnittenen für zwei Mengen A und B eingeführten Mengenoperationen werden noch die Differenzmenge oder Differenz die Diskrepanz oder symmetrische Differenz sowie das kartesische Produkt A x B erklärt.

1. Differenz zweier Mengen:
Die Menge der Elemente von , die nicht zu B gehören, heißt die Differenz oder Differenzmenge von A und B:
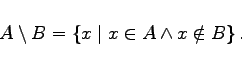(5.63a)

Wird A durch die Eigenschaft E1 und B durch die Eigenschaft E2 beschrieben, dann liegen in die Elemente, die zwar die Eigenschaft nicht aber die Eigenschaft E2 besitzen.
In der linken Abbildung ist die Differenz zweier Mengen schattiert dargestellt.

Beispiel

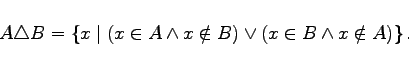2. Symmetrische Differenz zweier Mengen:
Die symmetrische Differenz ist die Menge aller Elemente, die zu genau einer der beiden Mengen A und B gehören:
(5.63b)

Aus der Definition folgt, daß gilt

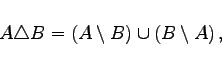(5.63c)

d.h. die symmetrische Differenz enthält die Eelemente, die genau eine der beiden Eigenschaften E1 (zu A) und E2 (zu B) besitzen. In der rechten Abbildung ist die symmetrische Differenz schattiert dargestellt.

Bild

Beispiel

3. Kartesisches Produkt zweier Mengen:
(5.64a)

Die Elemente (a,b) von A x B heißen geordnete Paare und sind durch

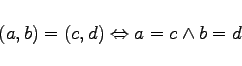(5.64b)

charakterisiert.
Die Anzahl der Elemente im kartesischen Produkt zweier endlicher Mengen beträgt

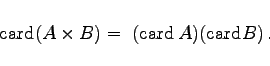(5.65)
Beispiel

Für A={1,2,3} und B={2,3} ergibt sich A x B = {(1,2),(1,3),(2,3),(2,3),(3,2),(3,3),} und B x A = {(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)} mit .
Beispiel

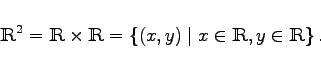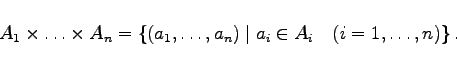Mit dem kartesischen Produkt  ( Menge der reellen Zahlen) kann man alle Punkte der x,y-Ebene beschreiben.
Die Menge der Koordinaten (x,y) wird durch dargestellt, denn es gilt:
4. Kartesisches Produkt aus n Mengen:
Aus n Elementen werden durch Festlegung einer bestimmten Reihenfolge (1. Element, 2. Element,...,n-tes Element) geordnete n-Tupel gebildet. Sind die Elemente, dann notiert man das n-Tupel als , wobei ai i-te Komponente genannt wird. Für n=3,4,5 spricht man von Tripel, Quadrupel und Quintupel.
Das n-fache kartesische Produkt ist dann die Menge aller geordneten n-Tupel mit
(5.66a)

Sind alle Ai endliche Mengen, dann beträgt die Anzahl der geordneten Elemente

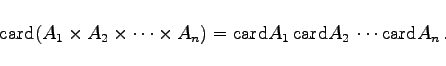(5.66b)

Hinweis: Das n-fache kartesische Produkt einer Menge A mit sich selbst wird mit An bezeichnet.