Inhalt Index DeskTop Bronstein
![]()
![]() Algebra und Diskrete Mathematik Fuzzy-Logik Fuzzy-wertige Relationen Fuzzy-Relationenprodukt
Algebra und Diskrete Mathematik Fuzzy-Logik Fuzzy-wertige Relationen Fuzzy-Relationenprodukt
Verwendet man über endlichen Grundbereichen eine Matrixdarstellung analog (5.391b), so läßt sich die Verknüpfung ![]() wie folgt motivieren: Es seien gegeben
wie folgt motivieren: Es seien gegeben ![]() und
und ![]() sowie die Matrixdarstellung von R,S in der Form R=(rij) und S=(sjk) mit
sowie die Matrixdarstellung von R,S in der Form R=(rij) und S=(sjk) mit ![]() sowie
sowie
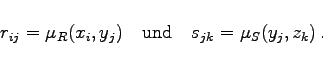 |
(5.397) |
Wird für die Verknüpfung ![]() die Matrixdarstellung tik gewählt, dann ist
die Matrixdarstellung tik gewählt, dann ist
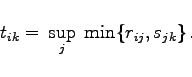 |
(5.398) |
Als Ergebnis erhält man nicht die übliche Form der Matrixmultiplikation, da die Supremumbildung anstelle der Summenbildung und die Minimumbildung anstelle der Produktbildung zur Anwendung kommen.
| Beispiel |
|
Mit den Darstellungen für rij und sjk sowie mit Gleichung (5.396) kann die inverse Relation R-1 durch die zu (rij) transponierte Matrix |