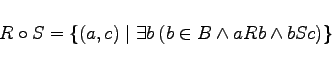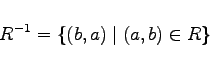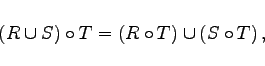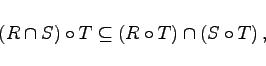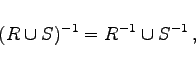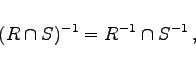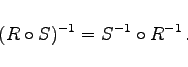Relationenprodukt, inverse Relation
Relationen sind spezielle Mengen, so daß zwischen Relationen die üblichen Mengenoperationen ausgeführt werden können. Für zweistellige Relationen sind darüber hinaus das Relationenprodukt und die inverse Relation von Bedeutung. Es seien 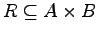 und
und 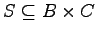 zweistellige Relationen. Dann ist das Produkt
zweistellige Relationen. Dann ist das Produkt  der Relationen R und S durch
der Relationen R und S durch
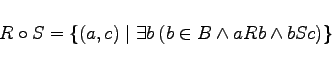 |
(5.68) |
definiert. Das Relationenprodukt ist assoziativ, aber nicht kommutativ.
Die inverse Relation R-1 einer Relation R ist durch
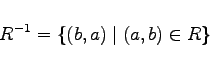 |
(5.69) |
festgelegt.
Für binäre Relationen in einer Menge A gelten folgende Beziehungen:
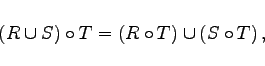 |
(5.70) |
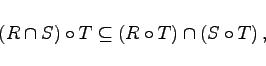 |
(5.71) |
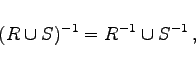 |
(5.72) |
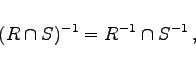 |
(5.73) |
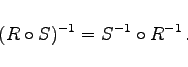 |
(5.74) |
![]()
![]() Algebra und Diskrete Mathematik Mengenlehre Relationen und Abbildungen
Algebra und Diskrete Mathematik Mengenlehre Relationen und Abbildungen
![]() und
und ![]() zweistellige Relationen. Dann ist das Produkt
zweistellige Relationen. Dann ist das Produkt ![]() der Relationen R und S durch
der Relationen R und S durch