Inhalt Index DeskTop Bronstein
![]()
![]() Algebra und Diskrete Mathematik Mengenlehre Relationen und Abbildungen
Algebra und Diskrete Mathematik Mengenlehre Relationen und Abbildungen
Eine Abbildung (oder Funktion) f von einer Menge A in eine Menge B (Bezeichnung ![]() ) ist eine Zuordnungsvorschrift, die jedem Element
) ist eine Zuordnungsvorschrift, die jedem Element ![]() eindeutig ein Element
eindeutig ein Element ![]() zuordnet. Man kann eine Abbildung f als zweistellige Relation zwischen A und
zuordnet. Man kann eine Abbildung f als zweistellige Relation zwischen A und ![]() auffassen:
auffassen: ![]() heißt Abbildung von A nach B, falls gilt:
heißt Abbildung von A nach B, falls gilt:
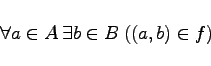 |
(5.82) |
und
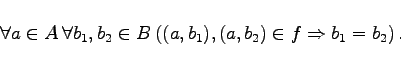 |
(5.83) |
Die Funktion f heißt eineindeutig (oder injektiv), falls zusätzlich gilt:
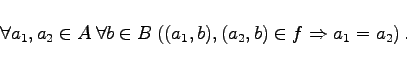 |
(5.84) |
Während bei einer Abbildung nur verlangt wird, daß jedes Original nur ein Bild hat, bedeutet Injektivität, daß auch jedes Bild nur ein Original besitzt.
Die Funktion f heißt Abbildung von A auf B (oder surjektiv), falls gilt:
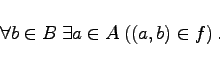 |
(5.85) |
Eine injektive und surjektive Abbildung heißt bijektiv. Für bijektive Abbildungen ![]() ist die inverse Relation eine Abbildung
ist die inverse Relation eine Abbildung ![]() die sogenannte Umkehrabbildung von f.
die sogenannte Umkehrabbildung von f.
Das Relationenprodukt, auf Abbildungen angewandt, charakterisiert die Hintereinanderausführung von Abbildungen: Sind ![]() und
und ![]() Abbildungen, so ist
Abbildungen, so ist ![]() eine Abbildung von A nach C, und es gilt
eine Abbildung von A nach C, und es gilt
Man beachte die Reihenfolge von f und g in dieser Gleichung (unterschiedliche Handhabung in der Literatur!).