Inhalt Index DeskTop Bronstein
![]()
![]() Algebra und Diskrete Mathematik Klassische algebraische Strukturen Lie-Gruppen
Algebra und Diskrete Mathematik Klassische algebraische Strukturen Lie-Gruppen
Die Elemente a einer kontinuierlichen Gruppe G können eindeutig und vollständig durch einen Satz reeller Parameter ![]() charakterisiert werden, von denen mindestens einer bei Durchlaufen der Gruppe kontinuierlich variiert. Die Anzahl n der Parameter wird als Ordnung oder Dimension d der kontinuierlichen Gruppe bezeichnet. Eine kontinuierliche Gruppe ist eine unendliche Gruppe.
charakterisiert werden, von denen mindestens einer bei Durchlaufen der Gruppe kontinuierlich variiert. Die Anzahl n der Parameter wird als Ordnung oder Dimension d der kontinuierlichen Gruppe bezeichnet. Eine kontinuierliche Gruppe ist eine unendliche Gruppe.
Jedes Gruppenelement ![]() entspricht einem Punkt
entspricht einem Punkt ![]() im n-dimensionalen Parameterraum
im n-dimensionalen Parameterraum ![]() . Durch die Festlegung, daß dem neutralen Element e der Gruppe G im Parameterraum das n-Tupel
. Durch die Festlegung, daß dem neutralen Element e der Gruppe G im Parameterraum das n-Tupel ![]() entspricht,
entspricht, ![]() , wird in
, wird in ![]() ein Koordinatensystem eingeführt. Jeder Umgebung U(a) eines Punktes P(a) im Parameterraum
ein Koordinatensystem eingeführt. Jeder Umgebung U(a) eines Punktes P(a) im Parameterraum ![]() entspricht einer Umgebung W(a) in der Gruppe
entspricht einer Umgebung W(a) in der Gruppe ![]() . Sind
. Sind ![]() und
und ![]() die Parameter des Gruppenelements a bzw. des inversen Elements
die Parameter des Gruppenelements a bzw. des inversen Elements ![]() , dann gilt für die Gruppenmultiplikation
, dann gilt für die Gruppenmultiplikation ![]() :
:
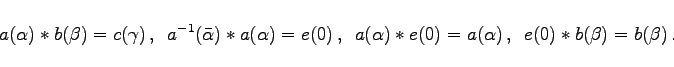 |
(5.131) |
| Beispiel |
|
Die zweidimensionalen Drehungen um einen festen Punkt in einer Ebene bilden eine kontinuierliche Gruppe der Dimension 1. Die Gruppenelemente R werden durch den Drehwinkel |
Die Einführung des Drehwinkels ![]() ist nicht die einzige Möglichkeit, die Gruppenlemente zu parametrisieren. Jede beliebige monotone Funktion
ist nicht die einzige Möglichkeit, die Gruppenlemente zu parametrisieren. Jede beliebige monotone Funktion ![]() könnte ebenfalls zur Charakterisierung der Gruppenelemente herangezogen werden.
könnte ebenfalls zur Charakterisierung der Gruppenelemente herangezogen werden.