Inhalt Index DeskTop Bronstein
![]()
![]() Unendliche Reihen Funktionenreihen Potenzreihen Definition der Potenzreihe, Konvergenz
Unendliche Reihen Funktionenreihen Potenzreihen Definition der Potenzreihe, Konvergenz
Gleichmäßig konvergent ist eine Potenzreihe in jedem abgeschlossenen Teilgebiet ![]() des Konvergenzbereiches (Satz von ABEL).
des Konvergenzbereiches (Satz von ABEL).
| Beispiel |
|
Für die Reihe |
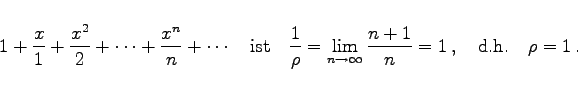 |
(7.78) |
Somit konvergiert die Reihe absolut in ![]() , für x = -1 ist sie bedingt konvergent (s. (7.34)) und für x = 1 divergiert sie (s. harmonische Reihe (7.16)). Gemäß dem Satz von ABEL handelt es sich um eine gleichmäßig konvergente Reihe in jedem Intervall
, für x = -1 ist sie bedingt konvergent (s. (7.34)) und für x = 1 divergiert sie (s. harmonische Reihe (7.16)). Gemäß dem Satz von ABEL handelt es sich um eine gleichmäßig konvergente Reihe in jedem Intervall ![]() , wobei
, wobei ![]() eine beliebige Zahl zwischen 0 und 1 ist.
eine beliebige Zahl zwischen 0 und 1 ist.